5

我很抱歉提前有点冗长：如果你想跳过所有的背景胡言乱语，你可以在下面看到我的问题。

这几乎是我之前发布的关于如何比较两个 1D（时间相关）信号的问题的后续。我得到的答案之一是我使用了互相关函数（MATLAB 中的 xcorr）。

背景资料

也许一些背景信息会很有用：我正在尝试实现独立分量分析算法。我的非正式测试之一是 (1) 通过 (a) 生成 2 个随机向量 (1x1000)，(b) 将向量组合成 2x1000 矩阵（称为“S”），然后将其乘以 2x2 混合来创建测试用例矩阵（称为“A”），给我一个新的矩阵（我们称之为“T”）。

总之：T = A * S

（2）然后我运行 ICA 算法来生成混合矩阵的逆（称为“W”），（3）将“T”乘以“W”来（希望）给我一个原始信号矩阵的重建（称为“X”）

总而言之：X = W * T

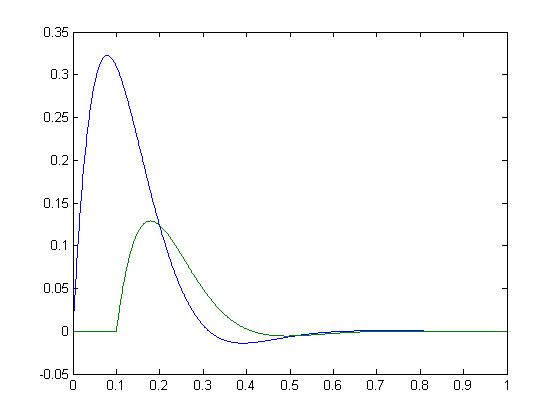
(4) 我现在想比较“S”和“X”。虽然“S”和“X”是 2x1000，但我只是比较S(1,:)和X(1,:)，S(2,:)每个X(2,:)都是 1x1000，使它们成为一维信号。（我还有一个步骤来确保这些向量是相互比较的正确向量，并且我还对信号进行了归一化）。

所以我目前的困惑是如何“评分”与 的S(1,:)匹配程度X(1,:)，以及与S(2,:)to的匹配程度X(2,:)。

到目前为止，我使用过类似的东西：r1 = max(abs(xcorr(S(1,:), X(1,:)))

我的问题

假设使用互相关函数是比较两个信号相似度的有效方法，那么对信号相似度进行分级的 R 值是多少？维基百科指出这是一个非常主观的领域，所以我听从那些可能在这个领域有经验的人的更好判断。

正如您可能意识到的那样，我根本不是来自 EE/DSP/统计背景（我是一名医学生），所以我现在正在经历一种“火中的洗礼”，我很感激所有我能得到的帮助。谢谢！

4

6 回答 6

12

（编辑：至于直接回答你关于 R 值的问题，见下文）

解决此问题的一种方法是使用互相关。请记住，您必须对幅度进行归一化并纠正延迟：如果您有信号 S1，并且信号 S2 的形状相同，但幅度只有一半并延迟了 3 个样本，它们仍然是完全相关的。

例如：

>> t = 0:0.001:1;
>> y = @(t) sin(10*t).*exp(-10*t).*(t > 0);
>> S1 = y(t);
>> S2 = 0.4*y(t-0.1);
>> plot(t,S1,t,S2);

替代文字

这些应该具有完美的相关系数。一种计算方法是使用最大互相关：

>> f = @(S1,S2) max(xcorr(S1,S2));

f = 

    @(S1,S2) max(xcorr(S1,S2))

>>  disp(f(S1,S1)); disp(f(S2,S2)); disp(f(S1,S2));
   12.5000

    2.0000

    5.0000

的最大值xcorr()负责信号之间的时间延迟。就幅度校正而言，您可以对信号进行归一化，使它们的自互相关为 1.0，或者您可以将等效步长折叠为以下：

ρ 2 = f(S1,S2) 2 / (f(S1,S1)*f(S2,S2);

在这种情况下 ρ 2 = 5 * 5 / (12.5 * 2) = 1.0

您可以求解 ρ 本身，即 ρ = f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2))，请记住 1.0 和 -1.0 完全相关（-1.0有相反的符号）

试试你的信号！

关于接受/拒绝使用什么阈值，这实际上取决于您拥有什么样的信号。0.9 及更高版本相当不错，但可能会产生误导。我会考虑查看减去相关版本后得到的残余信号。您可以通过查看 xcorr() 最大值的时间索引来做到这一点：

>> t = 0:0.001:1;
>> y = @(a,t) sin(a*t).*exp(-a*t).*(t > 0);
>> S1=y(10,t);
>> S2=0.4*y(9,t-0.1);
>> f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2))

ans =

    0.9959

这看起来非常适合相关性。但是让我们尝试用 S1 的缩放/移位倍数拟合 S2：

>> [A,i]=max(xcorr(S1,S2)); tshift = i-length(S1);
>> S2fit = zeros(size(S2)); S2fit(1-tshift:end) = A/f(S1,S1)*S1(1:end+tshift);
>> plot(t,[S2; S2fit]); % fit S2 using S1 as a basis

替代文字

>> plot(t,[S2-S2fit]);  % residual

替代文字

残差中有一些能量；要了解多少，您可以使用以下命令：

>> S2res=S2-S2fit;
>> dot(S2res,S2res)/dot(S2,S2)

ans =

    0.0081

>> sqrt(dot(S2res,S2res)/dot(S2,S2))

ans =

    0.0900

这表示残差具有原始信号 S2 的大约 0.81% 的能量（均方根幅度的 9%）。（一维信号与其自身的点积将始终等于该信号与其自身的互相关的最大值。）

我认为没有灵丹妙药可以回答两个信号彼此之间的相似程度，但希望我已经为您提供了一些可能适用于您的情况的想法。

于 2009-08-19T13:08:38.527 回答
1

一个好的起点是通过计算每个信号的自相关（即每个信号与其自身的“互相关”）来了解完美匹配的外观。

于 2009-08-17T20:18:36.087 回答
1

这是一个完整的猜测 - 但我猜 max(abs(xcorr(S(1,:),X(1,:)))) > 0.8 意味着成功。只是出于好奇，max(abs(xcorr(S(1,:),X(2,:)))) 的值是多少？

验证算法的另一种方法可能是比较 A 和 W。如果 W 计算正确，它应该是 A^-1，所以你可以计算像 | A*W- 我|？也许您必须通过A*W.

回到你最初的问题，我来自 DSP 背景，所以我可以处理相当无噪声的信号。我知道这不是您在生物学中获得的奢侈品 :) 所以我的 0.8 猜测可能非常乐观。也许查看您所在领域的一些文献，即使它们没有完全使用互相关，也可能有用。

于 2009-08-17T21:38:45.940 回答
1

通常在这种情况下，人们会谈论“错误接受率”和“错误拒绝率”。第一个描述了算法对非相似信号说“相似”的次数，第二个则相反。

因此，选择阈值成为这些标准之间的权衡。要使 FAR=0，阈值应为 1，要使 FRR=0，阈值应为 -1。

因此，您可能需要确定在您的情况下可以接受 FAR 和 FRR 之间的哪种权衡，这将为阈值提供正确的值。

从数学上讲，这可以用不同的方式表达。仅举几个例子： 1. 将一些速率固定在可接受的值并最小化其他速率 2. 最小化 max(FRR,FAR) 3. 最小化 a FRR+b FAR

于 2009-08-18T09:11:17.107 回答
0

由于它们应该相等，因此相关系数应该很高，介于 0.99 和 1 之间。我也会将 max 和 abs 函数从您的计算中剔除。

编辑：我说得太早了。我将互相关与相关系数混淆了，这是完全不同的。我的回答可能不值钱。

于 2009-08-17T18:23:41.700 回答
0

我同意结果是主观的。涉及逐个元素的差异平方和的东西将具有一定的价值。两个相同的数组将以该形式给出 0 值。您必须决定什么值会变成“坏”。组成两个“还不错”的不同向量，并找到它们的互相关系数作为指导。

（顺便说一句：如果你正在做一个相关系数，其中 1 或 -1 会很好，而 0 会很糟糕，生物统计学家告诉我，0.7 的实际值非常好。我知道这是不完全是你在做什么，但对相关系数的评论更早出现了。）

于 2009-08-17T20:30:48.510 回答